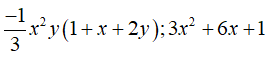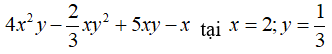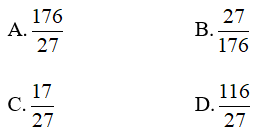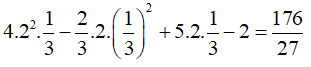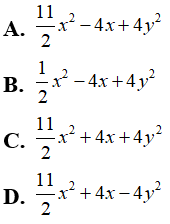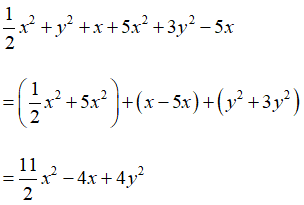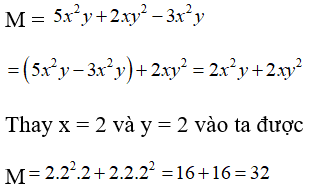Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức?

Đa thức là nội dung cơ bản để chúng ta có thể nghiên cứu lên các bài toán cao cấp hơn. Hãy cùng chúng tôi ôn tập lại kiến thức của đa thức thông qua bài viết dưới đây nhé!

1. Đa thức là gì?

Đa thức là tổng của các đơn thức. Mỗi đơn thức trong tổng được gọi là một hạng tử của đa thức đó.

Chú ý: Mỗi đơn thức được coi là một đa thức.

Ví dụ: x2 – 3; xyz–ax5 + by; a(3xy + 7x) là các đa thức.

2. Bậc của đa thức là gì?

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng rút gọn của đa thức đó

Ví dụ: Đa thức x6–2y5 + x4y5 + 1 có bậc 9; Đa thức 3xy2/2 có bậc 3.

3. Cách rút gọn đa thức:

Nếu trong đa thức có chứa các đơn thức đồng dạng thì ta thu gọn các đơn thức đồng dạng đó để được một đa thức thu gọn.

Đa thức được gọi là đã thu gọn nếu trong đa thức không còn hai hạng tử nào đồng dạng.

Để rút gọn đa thức về dạng rút gọn (không có 2 số hạng nào giống nhau), các em lần lượt làm theo các bước sau:

Bước 1: Nhóm các đơn thức đồng dạng với nhau.

Bước 2: Cộng, trừ các đơn thức đồng dạng trong từng nhóm.

Ví dụ: Thu gọn đa thức

[CHUẨN NHẤT] Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức

4. Sự khác biệt giữa đa thức và đơn thức:

Một đa thức là một biểu thức toán học được hình thành bởi tổng của các đơn thức.

Một đơn thức không thể có phép cộng hoặc phép trừ giữa các biến.

Bậc của đa thức là bậc của đơn thức lớn nhất.

5. Bậc của đa thức:

Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng rút gọn của đa thức

Ví dụ: Đa thức x6 – 2y5 + x4y5 + 1 có bậc 9; Đa thức 3xy2/2 có bậc 3.

Chú ý:

Số 0 còn gọi là đa thức khác không và không có bậc.

Khi tìm bậc của đa thức, trước hết ta phải rút gọn đa thức.

6. Các phép tính đa thức:

Đa thức là phép toán phức tạp, bởi vậy việc biến đổi các đa thức phức tạp về đa thức đơn giản chúng ta phải thông qua một số phép tính như sau:

Cộng đa thức

Để cộng hai đa thức ta lần lượt thực hiện các bước sau:

– Viết liên tiếp các hạng tử của hai đa thức cùng với dấu của chúng.

– Thu gọn các số hạng đồng dư (nếu có).

Ví dụ: Tính đa thức sau: (x + 3y) +(2x – y)

Ta kết hợp các số hạng của cùng một biến với nhau như sau:

(x + 3y) +(2x – y) = (x + 2x) + (3y – y) = 3x + 2y

Phép trừ đa thức

Để trừ hai đa thức ta lần lượt thực hiện các bước sau:

– Viết các hạng tử của đa thức bậc nhất cùng với dấu của chúng.

– Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại.

– Thu gọn các hạng tử đồng dạng (nếu có).

Ví dụ: Tính đa thức (x + y) – (2x – y)

Đa thức đầu tiên không dấu nên ta giữ nguyên, đa thức thứ hai có dấu trừ phía trước nên ta đổi dấu đơn thức trong ngoặc như sau:

(x + 3y) – (2x – y) = x + 3y – 2x + y = (x – 2x) + (3y + y) = -x + 4y

Phép nhân đa thức

Nhân đơn thức với đa thức: Thực hiện nhân đơn thức với từng hạng tử của đa thức sau đó cộng tổng lại với nhau.

Công thức: A(B + C) = AB + AC

Ví dụ: x(10y + 5) = 10xy + 5x

Nhân đa thức với đa thức: Thực hiện nhân lần lượt từng hạng tử của đa thức này với từ hạng của đa thức kia, sau đó cộng tổng của cả hai lại với nhau.

Công thức: (A + B)(C + D) = AC + AD + BC + BD

Ví dụ: (2x + 3)(4y + 5) = 10x + 8xy + 12y + 15

Phép chia đa thức

Chia đa thức cho đơn thức: Thực hiện chia lần lượt từng hạng tử của đa thức cho đơn thức sau đó cộng tổng lại với nhau.

Ví dụ:

[CHUẨN NHẤT] Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức (ảnh 2) — *Ví dụ về chia đa thức cho đơn thức*

Chia đa thức cho đa thức: Thực hiện sắp xếp đa thức theo lũy thừa giảm dần của biến, sau đó thực hiện phép chia.

7. Bài tập vận dụng:

Bài 1: Tìm bậc của đa thức

[CHUẨN NHẤT] Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức (ảnh 4)

Bài 2: Tính giá trị của các đa thức

[CHUẨN NHẤT] Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức (ảnh 5)

[CHUẨN NHẤT] Đa thức là gì? Bậc của đa thức là gì? Cách thu gọn đa thức (ảnh 6)

Bài 1: Cho các biểu thức

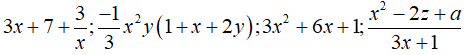Trắc nghiệm: Đa thức (a là hằng số).

Có bao nhiêu đa thức trong các biểu thức trên?

A. 2

B. 1

C. 3

D. 4

Các biểu thức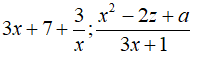 Trắc nghiệm: Đa thức đều chứa các biến ở mẫu nên không phải đa thức

Có hai đa thức là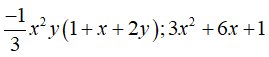 Trắc nghiệm: Đa thức

Chọn đáp án A

Bài 2: Sắp xếp đa thức 2x + 5x³ – x² + 5x⁴ theo lũy thừa giảm dần của biến x

A. 5x⁴ – x² + 5x³ + 2x

B. 2x – x² + 5³ + 5x⁴

C. 5x⁴ + 5x³ + x² – 2x

D. 5x⁴ + 5x³ – x² + 2x

Ta có 2x + 5x³ – x² + 5x⁴ = 5x⁴ + 5x³ – x² + 2x

Chọn đáp án D

Bài 3: Bậc của đa thức xy + xy⁵ + x⁵yz là

A. 6

B. 7

C. 5

D. 4

Bậc của đa thức xy + xy⁵ + x⁵yz là 5 + 1 + 1 = 7

Chọn đáp án B

Bài 4: Thu gọn đa thức 4x²y + 6x³y² – 10x²y + 4x³y²

A. 14x²y + 10x³y²

B. -14x²y + 10x³y²

C. 6x²y – 10x³y²

D. -6x²y + 10x³y²

Ta có: 4x²y + 6x³y² – 10x²y + 4x³y²

= (4x²y – 10x²y ) + (6x³y² + 4x³y²) = -6x²y + 10x³y²

Chọn đáp án D

Bài 5: Thu gọn và tìm bậc của đa thức 12xyz – 3x⁵ + y⁴ + 3xyz + 2x⁵ ta được

A. Kết quả là đa thức -2x⁵ + 15xyz + y⁴ có bậc là 4

B. Kết quả là đa thức -2x⁵ + 15xyz + y⁴ có bậc là 5

C. Kết quả là đa thức -x⁵ + 15xyz + y⁴ có bậc là 4

D. Kết quả là đa thức -x⁵ – 15xyz + y⁴ có bậc là 4

Ta có 12xyz – 3x⁵ + y⁴ + 3xyz + 2x⁵

= (-3x⁵ + 2x⁵) + (12xyz + 3xyz) + y⁴ = -x⁵ + 15xyz + y⁴

Bậc của đa thức -x⁵ + 15xyz + y⁴ là 5

Chọn đáp án B

Bài 6: Giá trị của biểu thức

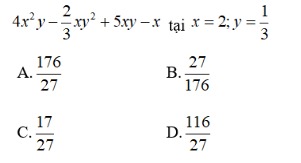
Trắc nghiệm: Đa thức

Thay x = 2, y = 1/3 vào đa thức 4x²y – (2/3)xy² + 5xy -x ta được

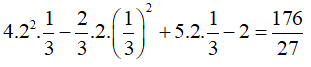
Trắc nghiệm: Đa thức

Chọn đáp án A

II. Bài tập tự luận

Bài 1: Tìm bậc của đa thức

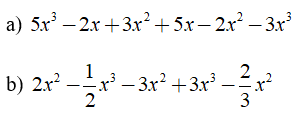
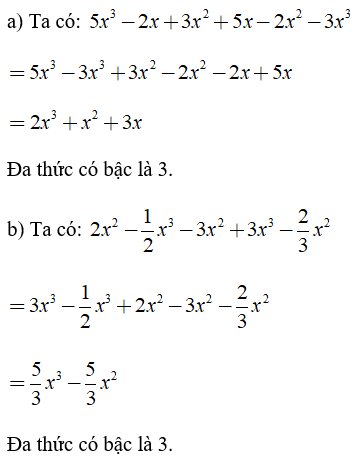
Trắc nghiệm: Đa thức

Đáp án

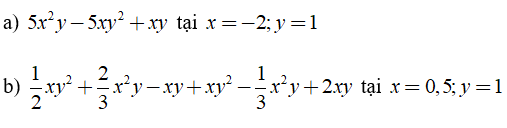
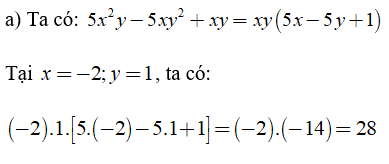
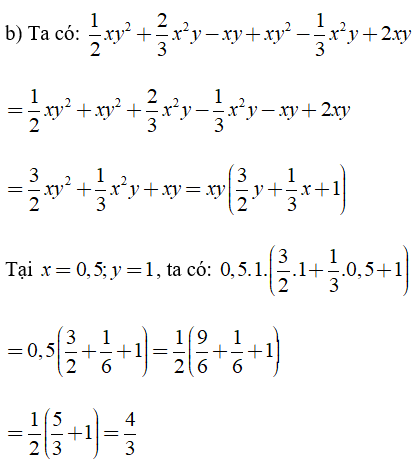
Bài 1: Cho các biểu thức

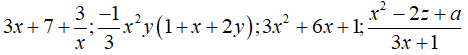
Trắc nghiệm Đa thức - Bài tập Toán lớp 7 chọn lọc có đáp án, lời giải chi tiết ( a là hằng số ).

Có bao nhiêu đa thức trong các biểu thức trên?

A. 2 B. 1 C. 3 D. 4

Hướng dẫn giải:

Các biểu thức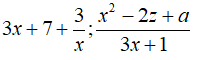 Trắc nghiệm Đa thức - Bài tập Toán lớp 7 chọn lọc có đáp án, lời giải chi tiết đều chứa các biến ở mẫu nên không phải đa thức

Có hai đa thức là Trắc nghiệm Đa thức - Bài tập Toán lớp 7 chọn lọc có đáp án, lời giải chi tiết

Chọn đáp án A

Bài 2: Sắp xếp đa thức 2x + 5x³ – x² + 5x⁴ theo lũy thừa giảm dần của biến x

A. 5x⁴ – x² + 5x³ + 2x

B. 2x – x² + 5³ + 5x⁴

C. 5x⁴ + 5x³ + x² – 2x

D. 5x⁴ + 5x³ – x² + 2x

Hướng dẫn giải:

Ta có 2x + 5x³ – x² + 5x⁴ = 5x⁴ + 5x³ – x² + 2x

Chọn đáp án D

Bài 3: Bậc của đa thức xy + xy⁵ + x⁵yz là

A. 6 B. 7 C. 5 D. 4

Hướng dẫn giải:

Bậc của đa thức xy + xy⁵ + x⁵yz là 5 + 1 + 1 = 7

Chọn đáp án B

Bài 4: Thu gọn đa thức 4x²y + 6x³y² – 10x²y + 4x³y²

A. 14x²y + 10x³y²

B. -14x²y + 10x³y²

C. 6x²y – 10x³y²

D. -6x²y + 10x³y²

^{Hướng dẫn giải:}

Ta có: 4x²y + 6x³y² – 10x²y + 4x³y²

= (4x²y – 10x²y ) + (6x³y² + 4x³y²) = -6x²y + 10x³y²

Chọn đáp án D

Bài 5: Thu gọn và tìm bậc của đa thức 12xyz – 3x⁵ + y⁴ + 3xyz + 2x⁵ ta được

A. Kết quả là đa thức -2x⁵ + 15xyz + y⁴ có bậc là 4

B. Kết quả là đa thức -2x⁵ + 15xyz + y⁴ có bậc là 5

C. Kết quả là đa thức -x⁵ + 15xyz + y⁴ có bậc là 4

D. Kết quả là đa thức -x⁵ – 15xyz + y⁴ có bậc là 4

Ta có 12xyz – 3x⁵ + y⁴ + 3xyz + 2x⁵

= (-3x⁵ + 2x⁵) + (12xyz + 3xyz) + y⁴ = -x⁵ + 15xyz + y⁴

Bậc của đa thức -x⁵ + 15xyz + y⁴ là 5

Chọn đáp án B

Bài 6: Giá trị của biểu thức

Trắc nghiệm Đa thức - Bài tập Toán lớp 7 chọn lọc có đáp án, lời giải chi tiết

Thay x = 2, y = 1/3 vào đa thức 4x²y – (2/3)xy² + 5xy -x ta được

Trắc nghiệm Đa thức - Bài tập Toán lớp 7 chọn lọc có đáp án, lời giải chi tiết

Chọn đáp án A

Bài 7: Thu gọn đa thức 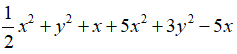Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án ta được

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Ta có:

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Chọn đáp án A

Bài 8: Bậc của đa thức 2002x²y³z + 2x³y²z² + 7x²y³z là

A. 5

B. 6

C. 7

D. 8

Ta có: Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Suy ra đa thức có bậc là 3 + 2 + 2 = 7

Vậy đa thức đã cho có bậc là 7.

Chọn đáp án C

Bài 9: Tính giá trị của biểu thức M = 5x²y + 2xy² – 3x² y tại x = 2 và y = 2

A. M = 30

B. M = 31

C. M = -31

D. M = 32

Ta có:

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Vậy giá trị của biểu thức M tại x = 2 và y = 2 là 32.

Chọn đáp án D

Câu 10: Sắp xếp đa thức $3{x^3} - 6x + 7{x^2} - 4$ theo lũy thừa giảm dần của biến

A. $3{x^3} + 7{x^2} - 6x - 4$ B. $3{x^3} - 6x + 7{x^2} - 4$

C. $- 6x + 7{x^2} - 4 + 3{x^2}$ D. $- 4 - 6x + 7{x^2} + 3x$

Câu 11: Bậc của đa thức ${mathop{rm xy}nolimits} + x{y^2} + x{y^6} + {x^2}{y^5}$ là

A. 5 B. 6 C. 7 D. 8

Câu 12: Thu gọn đa thức $4{x^2}y + 6{x^3}{y^2} - 10{x^2}y + 4{x^3}{y^2}$ ta được

A. $5{x^2}y + 7{x^3}{y^2}$ B. $- 10{x^2}y + 10{x^3}{y^2}$

C. $- 6{x^2}y + 6{x^3}{y^2}$ D. $- 6{x^2}y + 10{x^3}{y^2}$

Gọi Hotline 1900.0191

Công ty Luật LVN - Địa chỉ: Số 16B Nguyễn Thái Học, Yết Kiêu, Hà Đông, Hà Nội, Việt Nam